Pengertian Persamaan Diferensial

Pengertian Persamaan Diferensial: Jenis dan Penyelesaiannya

oleh

Pengertian Persamaan Diferensial – Persamaan diferensial adalah salah satu konsep yang sangat penting dalam matematika dan ilmu pengetahuan terapan. Persamaan diferensial menggambarkan hubungan antara suatu fungsi dan turunan-turunan fungsinya.

Konsep ini telah digunakan dalam berbagai bidang, termasuk fisika, kimia, ekonomi, dan biologi, untuk memodelkan dan memahami fenomena alamiah yang kompleks.

Apa Itu Persamaan Diferensial?

Persamaan diferensial adalah persamaan matematika yang melibatkan fungsi-fungsi tak hingga banyaknya dan turunan-turunan mereka. Persamaan ini menggambarkan hubungan antara suatu fungsi dan turunan-turunannya terhadap variabel independen yang terlibat.

Persamaan diferensial sering digunakan dalam ilmu pengetahuan terapan, seperti fisika, kimia, biologi, dan ekonomi, untuk memodelkan dan memahami fenomena alamiah yang kompleks.

Secara umum, persamaan diferensial dapat dituliskan dalam bentuk:

F(x, y, y’, y”, …, y^(n)) = 0

di mana x adalah variabel independen, y adalah fungsi yang ingin dicari, dan y’, y”, …, y^(n) adalah turunan-turunan fungsi y terhadap x hingga orde n. Persamaan ini dapat melibatkan turunan pertama, kedua, atau turunan orde tinggi lainnya.

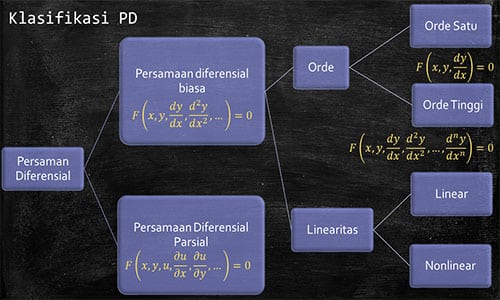
Persamaan diferensial dapat dikelompokkan menjadi dua jenis utama: persamaan diferensial biasa (ordinary differential equation, ODE) dan persamaan diferensial parsial (partial differential equation, PDE).

Persamaan diferensial biasa (ODE) melibatkan fungsi-fungsi satu variabel independen. Persamaan diferensial ini dapat menjadi linier atau nonlinier, tergantung pada hubungan antara fungsi dan turunan-turunannya. Contoh ODE yang sederhana adalah persamaan diferensial linier orde pertama:
dy/dx + P(x)y = Q(x)

di mana P(x) dan Q(x) adalah fungsi-fungsi yang tergantung pada x.

Persamaan diferensial parsial (PDE) melibatkan fungsi-fungsi lebih dari satu variabel independen. Persamaan diferensial ini melibatkan turunan parsial dari fungsi terhadap variabel-variabel independen tersebut.

PDE sering digunakan dalam pemodelan fenomena yang melibatkan perubahan dalam ruang dan waktu. Contoh PDE yang umum adalah Persamaan Panas (Heat Equation) dan Persamaan Laplace.

Penyelesaian persamaan diferensial melibatkan mencari fungsi-fungsi yang memenuhi persamaan tersebut.

Terdapat berbagai metode yang digunakan untuk menyelesaikan persamaan diferensial, baik secara analitik maupun numerik, tergantung pada sifat dan kompleksitas persamaan tersebut.

Sejarah Persamaan Diferensial

Sejarah persamaan diferensial dimulai pada abad ke-17 dengan kontribusi matematikawan terkemuka seperti Isaac Newton dan Gottfried Wilhelm Leibniz. Berikut adalah gambaran umum tentang perkembangan sejarah persamaan diferensial:

1. Abad ke-17

  • Pada tahun 1665, Isaac Newton mengembangkan kalkulus dan metode diferensial yang menjadi landasan bagi persamaan diferensial.
  • Newton juga mengembangkan persamaan diferensial yang terkenal, seperti Persamaan Gerak Newton yang mendeskripsikan gerakan benda di bawah pengaruh gaya.

2. Abad ke-18

  • Joseph-Louis Lagrange dan Leonhard Euler berkontribusi dalam pengembangan metode analitis dan solusi persamaan diferensial.
  • Daniel Bernoulli memperkenalkan persamaan diferensial pada fluida (yang dikenal sebagai Persamaan Bernoulli) dan mempelajari aliran fluida melalui pipa dan saluran.

3. Abad ke-19

  • Jean-Baptiste Joseph Fourier memperkenalkan seri Fourier, yang digunakan untuk memecahkan persamaan diferensial suhu pada benda padat.
  • Pierre-Simon Laplace mempelajari persamaan diferensial untuk fenomena fisika seperti osilasi, dan mengembangkan transformasi Laplace yang penting dalam penyelesaian persamaan diferensial.

4. Abad ke-19 hingga ke-20

  • Carl Gustav Jacobi, Niels Henrik Abel, dan Karl Weierstrass mengembangkan teori persamaan diferensial lebih lanjut dengan memperkenalkan konsep teori fungsi dan analisis kompleks.
  • Henri Poincaré membuat kontribusi besar dalam pemahaman sistem dinamik dan teori kestabilan.

5. Abad ke-20 hingga saat ini

  • Teori kualitatif persamaan diferensial dikembangkan oleh matematikawan seperti Henri Cartan, Vladimir Arnold, dan Stephen Smale.
  • Perkembangan komputer dan metode numerik mengubah cara persamaan diferensial dianalisis dan diselesaikan secara praktis.

Pemodelan matematika dengan persamaan diferensial diterapkan luas di berbagai bidang ilmu pengetahuan dan teknik, termasuk fisika, biologi, ekonomi, dan rekayasa.

Perkembangan sejarah persamaan diferensial terus berlanjut dengan kontribusi matematikawan dan peneliti modern.

Teori dan metode baru terus dikembangkan untuk memecahkan persamaan diferensial yang lebih kompleks dan untuk memahami fenomena alamiah dengan lebih baik.

Persamaan diferensial tetap menjadi alat penting dalam pemodelan matematika dan analisis sistem dinamik di berbagai disiplin ilmu.

Jenis-jenis Persamaan Diferensial

Terdapat beberapa jenis persamaan diferensial yang umum digunakan, berdasarkan karakteristik dan sifat persamaan tersebut. Berikut ini adalah beberapa jenis-jenis persamaan diferensial yang penting:

1. Persamaan Diferensial Biasa (Ordinary Differential Equation, ODE)

Persamaan diferensial biasa melibatkan fungsi-fungsi satu variabel independen. ODE digunakan untuk memodelkan fenomena yang melibatkan satu variabel, seperti perubahan waktu.

    ODE dapat dikelompokkan menjadi beberapa jenis berdasarkan orde dan bentuk persamaannya, seperti ODE linier orde pertama, ODE linier orde tinggi, ODE nonlinier, ODE eksak, dan lain-lain.

    2. Persamaan Diferensial Parsial (Partial Differential Equation, PDE)

    Persamaan diferensial parsial melibatkan fungsi-fungsi lebih dari satu variabel independen. PDE digunakan untuk memodelkan fenomena yang melibatkan perubahan dalam ruang dan waktu, seperti perambatan gelombang, difusi, dan keseimbangan termal.

      PDE dapat dikelompokkan berdasarkan jenis persamaannya, seperti Persamaan Panas (Heat Equation), Persamaan Laplace, Persamaan Gelombang (Wave Equation), Persamaan Difusi (Diffusion Equation), Persamaan Maxwell, dan banyak lagi.

      3. Persamaan Diferensial Linier

      Persamaan diferensial linier adalah persamaan diferensial di mana fungsi-fungsi dan turunan-turunan mereka muncul dalam bentuk linier.

        Persamaan linier dapat dipecahkan secara analitik dengan menggunakan metode-metode khusus seperti metode pemisahan variabel, metode faktor pengali, atau transformasi Laplace. Persamaan diferensial linier banyak digunakan dalam berbagai bidang ilmu pengetahuan dan rekayasa.

        4. Persamaan Diferensial Nonlinier

        Persamaan diferensial nonlinier adalah persamaan diferensial di mana fungsi-fungsi dan turunan-turunan mereka muncul dalam bentuk nonlinier.

        Persamaan diferensial nonlinier sering kali lebih sulit untuk dianalisis dan diselesaikan dibandingkan persamaan diferensial linier.

          Solusi persamaan diferensial nonlinier dapat ditemukan menggunakan metode numerik atau pendekatan aproksimasi.

          5. Persamaan Diferensial Stokastik

          Persamaan diferensial stokastik melibatkan unsur keacakan atau fluktuasi. Persamaan diferensial stokastik digunakan untuk memodelkan fenomena yang dipengaruhi oleh faktor-faktor acak, seperti pergerakan Brownian dan dinamika populasi.

            Penyelesaian persamaan diferensial stokastik melibatkan konsep probabilitas dan metode khusus seperti persamaan Ito atau persamaan Langevin.

            Setiap jenis persamaan diferensial memiliki metode penyelesaian yang khusus dan alat matematika yang relevan. Pilihan jenis persamaan diferensial yang tepat tergantung pada sifat fenomena yang ingin dimodelkan dan analisis yang ingin dilakukan.

            Penyelesaian Persamaan Diferensial

            Penyelesaian persamaan diferensial melibatkan mencari fungsi-fungsi yang memenuhi persamaan tersebut.

            Terdapat berbagai metode yang digunakan untuk menyelesaikan persamaan diferensial, tergantung pada sifat persamaan dan jenisnya.

            Berikut ini adalah beberapa metode umum yang digunakan dalam penyelesaian persamaan diferensial:

            1. Metode Analitik

            Metode analitik mencoba mencari solusi eksak persamaan diferensial dalam bentuk fungsi matematika yang diketahui. Beberapa metode analitik yang umum digunakan meliputi:

              • Metode Pemisahan Variabel: Metode ini digunakan untuk persamaan diferensial biasa (ODE) linier yang dapat dipisahkan menjadi dua fungsi yang masing-masing tergantung pada variabel independen dan variabel dependen. Dengan memisahkan variabel-variabel ini, persamaan dapat diselesaikan dengan integrasi.
              • Metode Faktor Pengali: Metode ini digunakan untuk persamaan diferensial linier yang dapat diubah menjadi persamaan diferensial linier homogen dengan mengalikan faktor eksponensial yang tepat. Setelah itu, persamaan homogen dapat diselesaikan dengan metode pemisahan variabel atau metode lainnya.
              • Metode Transformasi: Metode ini melibatkan transformasi khusus pada persamaan diferensial untuk mengubahnya menjadi persamaan diferensial yang lebih mudah diselesaikan. Contoh transformasi yang umum digunakan adalah transformasi Laplace dan transformasi Fourier.
              • Metode Variasi Parameter: Metode ini digunakan untuk persamaan diferensial linier nonhomogen dengan menggunakan fungsi variabel bebas sebagai parameter. Dengan memilih parameter yang tepat, solusi partikular dapat ditemukan melalui proses integrasi.

              2. Metode Numerik

              Metode numerik digunakan ketika tidak ada solusi eksak yang diketahui atau ketika persamaan diferensial nonlinier atau kompleks.

                Metode numerik mengandalkan komputasi dan pendekatan nilai-nilai solusi menggunakan algoritma dan teknik komputasi. Beberapa metode numerik yang umum digunakan meliputi:

                • Metode Euler: Metode ini merupakan metode numerik yang sederhana dan digunakan untuk menyelesaikan persamaan diferensial biasa (ODE). Metode Euler mengaproksimasi turunan dengan menggunakan suku pertama deret Taylor.
                • Metode Runge-Kutta: Metode Runge-Kutta adalah metode numerik yang lebih akurat untuk menyelesaikan persamaan diferensial biasa (ODE). Metode ini menggunakan beberapa langkah iterasi untuk menghitung pendekatan solusi.
                • Metode Elemen Hingga: Metode ini digunakan untuk menyelesaikan persamaan diferensial parsial (PDE) dengan membagi domain solusi menjadi elemen-elemen diskrit. Persamaan diferensial kemudian dikonversi menjadi sistem persamaan linear dengan menggunakan fungsi-fungsi dasar yang sesuai pada setiap elemen.

                Selain metode-metode di atas, terdapat juga metode-metode lain seperti metode Fourier, metode integral, metode iteratif, dan lain-lain, yang digunakan tergantung pada sifat persamaan diferensial yang akan diselesaikan.

                Penting untuk diingat bahwa penyelesaian persamaan diferensial dapat melibatkan langkah-langkah matematika yang rumit dan terkadang memerlukan pemahaman yang mendalam tentang teori persamaan diferensial.

                Dalam kasus persamaan diferensial yang kompleks atau tidak dapat diselesaikan secara analitik, metode numerik sering menjadi pilihan yang lebih praktis untuk mendapatkan solusi numerik yang akurat.

                Penerapan Persamaan Diferensial

                Persamaan diferensial memiliki berbagai penerapan dalam berbagai bidang ilmu pengetahuan dan rekayasa.

                Mereka digunakan untuk memodelkan fenomena alamiah yang kompleks dan menggambarkan hubungan antara variabel dan turunan-turunannya. Berikut ini adalah beberapa penerapan penting dari persamaan diferensial:

                1. Fisika

                Persamaan diferensial digunakan secara luas dalam fisika untuk memodelkan dan menganalisis fenomena fisika.

                  Contohnya termasuk persamaan gerak Newton, persamaan Maxwell dalam elektrodinamika, persamaan Schrödinger dalam mekanika kuantum, persamaan panas untuk perambatan panas, persamaan gelombang untuk perambatan gelombang, dan banyak lagi.

                  Persamaan diferensial membantu dalam memahami pergerakan benda, osilasi, sistem dinamik, medan elektromagnetik, dan banyak aspek fisika lainnya.

                  2. Matematika Keuangan

                  Persamaan diferensial digunakan dalam matematika keuangan untuk menganalisis dan memodelkan pasar keuangan, harga opsi, portofolio investasi, dan pergerakan harga aset.

                    Persamaan diferensial stokastik khusus digunakan untuk mempertimbangkan fluktuasi harga dan faktor acak lainnya dalam perhitungan nilai-nilai keuangan.

                    3. Biologi

                    Persamaan diferensial memiliki banyak aplikasi dalam biologi untuk memodelkan dan memahami fenomena biologis.

                      Mereka digunakan untuk mempelajari dinamika populasi, interaksi antara spesies, pertumbuhan dan perkembangan organisme, sistem kekebalan tubuh, perubahan genetik, proses biokimia, dan banyak lagi.

                      Persamaan diferensial membantu dalam memahami perubahan dan interaksi kompleks dalam sistem biologis.

                      4. Kimia

                      Persamaan diferensial digunakan dalam kimia untuk memodelkan reaksi kimia, kinetika reaksi, perpindahan panas dan massa dalam sistem kimia.

                        Mereka membantu dalam memahami laju reaksi, distribusi konsentrasi, evolusi suhu, dan perubahan komposisi kimia dalam sistem yang kompleks. Persamaan diferensial juga digunakan dalam pemodelan reaktor kimia dan proses industri kimia.

                        5. Rekayasa

                        Persamaan diferensial digunakan secara luas dalam rekayasa untuk memodelkan dan menganalisis sistem kontrol, sistem mekanik, sistem termal, sistem listrik, dan proses optimisasi.

                          Mereka membantu dalam merancang sistem yang efisien, memahami respons sistem terhadap sinyal input, memprediksi perilaku sistem, dan mengoptimalkan kinerja sistem.

                          Selain bidang-bidang di atas, persamaan diferensial juga diterapkan dalam astronomi, meteorologi, ekonomi, ilmu material, ilmu lingkungan, ilmu kedokteran, dan banyak bidang lainnya.

                          Mereka adalah alat penting dalam pemodelan dan analisis fenomena alamiah yang kompleks, membantu kita memahami dunia di sekitar kita dengan lebih baik.

                          Demikian artikel kali ini. Semoga artikel ini dapat membantu kamu untuk mempelajari Persamaan Diferensial lebih baik lagi. Sampai jumpa di artikel selanjutnya.

                          Baca juga artikel lainnya :