Pengertian Teorema Pythagoras – Teorema Pythagoras adalah salah satu teorema paling terkenal dan penting dalam matematika. Teorema ini memberikan hubungan fundamental antara panjang sisi-sisi segitiga siku-siku.
Ditemukan oleh matematikawan Yunani kuno bernama Pythagoras, teorema ini memiliki aplikasi luas dalam berbagai aspek matematika, fisika, dan rekayasa. Artikel ini akan mengulas konsep, bukti, dan aplikasi teorema Pythagoras.
Apa Itu Teorema Pythagoras?
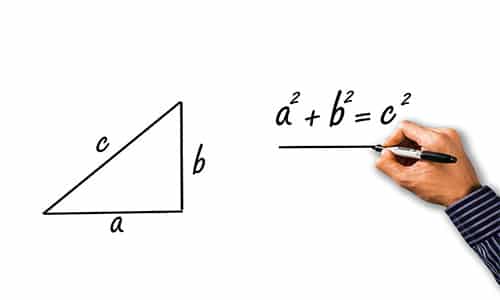
Teorema Pythagoras adalah salah satu prinsip fundamental dalam geometri yang menghubungkan panjang sisi-sisi dalam segitiga siku-siku.
Ditemukan oleh matematikawan Yunani kuno bernama Pythagoras, teorema ini memiliki banyak aplikasi dalam matematika, fisika, dan berbagai bidang ilmu lainnya.
Teorema Pythagoras menyatakan hubungan antara panjang sisi-sisi dalam segitiga siku-siku sebagai berikut:
“Di dalam segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang dua sisi yang membentuk sudut siku.”
Secara matematis, teorema Pythagoras dapat dirumuskan sebagai berikut:
�2=�2+�2c2=a2+b2
Dalam rumus ini:
- �c adalah panjang sisi miring (hipotenusa) segitiga.
- �a adalah panjang salah satu sisi yang membentuk sudut siku.
- �b adalah panjang sisi lainnya yang juga membentuk sudut siku.
Artinya, panjang kuadrat hipotenusa (�2c2) sama dengan jumlah kuadrat panjang kedua sisi yang membentuk sudut siku (�2a2 dan �2b2).
Ini adalah konsep yang mendasar dalam geometri dan digunakan untuk menghitung panjang sisi-sisi dalam segitiga siku-siku, mengidentifikasi segitiga siku-siku, dan dalam berbagai aplikasi praktis dalam ilmu pengetahuan dan teknologi.
Teorema Pythagoras adalah salah satu dari sedikit teorema dalam matematika yang sangat terkenal dan sering digunakan dalam kehidupan sehari-hari, terutama dalam konteks pengukuran dan perhitungan panjang sisi-sisi segitiga.
Sejarah Teorema Pythagoras
Sejarah Teorema Pythagoras dapat ditelusuri kembali ke zaman kuno, sekitar abad ke-6 atau ke-5 SM. Meskipun tidak ada catatan tertulis langsung dari Pythagoras sendiri, teorema ini dikenal sebagai Teorema Pythagoras berdasarkan nama matematikawan Yunani kuno, Pythagoras, yang dianggap sebagai penemu dan pemimpin aliran filsafat Pythagorean.
Dalam tradisi Pythagorean, penemuan teorema ini sering dikaitkan dengan seorang matematikawan bernama Pythagoras, yang hidup sekitar abad ke-6 SM di pulau Samos, Yunani. Pythagoras dan pengikutnya merupakan kelompok yang tertarik pada matematika, filsafat, dan agama.
Mereka memandang matematika sebagai ilmu yang suci dan melihat hubungan antara angka dan alam semesta sebagai manifestasi prinsip-prinsip fundamental.
Oleh karena itu, dikatakan bahwa Pythagoras menemukan dan mengembangkan Teorema Pythagoras sebagai bagian dari eksplorasi matematika dan spiritualitasnya.
Namun, penemuan teorema ini tidak eksklusif bagi Pythagoras. Bukti tertua tentang teorema ini ditemukan dalam papirus Mesir yang berasal dari sekitar 2000 SM. Papirus tersebut mencantumkan beberapa contoh yang menunjukkan pemahaman tentang hubungan antara sisi-sisi segitiga siku-siku.
Selain itu, bukti teorema Pythagoras juga ditemukan dalam literatur matematika India dan Babilonia yang lebih tua.
Meskipun ada bukti-bukti awal dari berbagai peradaban, Pythagoras dikenal karena popularitasnya dalam menyebarkan pengetahuan matematika dan mengaitkan teorema ini dengan pengajaran dan filosofi aliran Pythagorean.
Pengetahuan tentang teorema ini dipelajari dan dikembangkan lebih lanjut oleh para pengikut Pythagoras, serta generasi matematikawan dan filsuf Yunani berikutnya, termasuk Euclid, yang menulis bukti formal tentang teorema ini dalam bukunya “Elemen”.
Seiring waktu, Teorema Pythagoras menjadi salah satu konsep matematika yang paling penting dan terkenal di dunia. Penerapannya meluas ke berbagai bidang ilmu dan terus digunakan hingga saat ini.
Meskipun kita tidak dapat mengetahui secara pasti siapa yang menemukan teorema ini pertama kali, kontribusi Pythagoras dalam mengembangkan dan mengajarkan teorema ini membuatnya dikenal dan dihormati sebagai tokoh yang terkait dengan teorema Pythagoras dalam sejarah matematika.
Penggunaan Teorema Pythagoras
Teorema Pythagoras memiliki banyak penggunaan praktis dalam berbagai bidang. Berikut ini adalah beberapa contoh penggunaan teorema Pythagoras:
1. Menghitung Panjang Sisi
Salah satu penggunaan utama teorema Pythagoras adalah untuk menghitung panjang sisi dalam segitiga siku-siku.
Jika panjang dua sisi diketahui, teorema ini dapat digunakan untuk mencari panjang sisi yang ketiga. Misalnya, jika panjang sisi a = 3 dan b = 4, kita dapat menggunakan teorema Pythagoras (a^2 + b^2 = c^2) untuk mencari panjang sisi hipotenusa (c).
2. Membuktikan Sifat Segitiga Siku-siku
Teorema Pythagoras juga digunakan untuk membuktikan apakah suatu segitiga adalah segitiga siku-siku.
Jika kuadrat panjang sisi-sisi yang diketahui memenuhi persamaan teorema Pythagoras, maka segitiga tersebut dapat dianggap sebagai segitiga siku-siku.
3. Menentukan Sudut dalam Segitiga
Dalam segitiga siku-siku, teorema Pythagoras dapat digunakan untuk menentukan ukuran sudut tertentu.
Misalnya, jika panjang dua sisi diketahui, teorema ini dapat digunakan untuk menghitung sudut yang terbentuk oleh kedua sisi tersebut.
4. Arsitektur dan Konstruksi
Dalam bidang arsitektur dan konstruksi, teorema Pythagoras digunakan untuk memastikan sudut-sudut yang tepat dan membangun struktur yang seimbang.
Misalnya, untuk membangun dinding dengan sudut 90 derajat, teorema Pythagoras digunakan untuk memastikan bahwa panjang sisi-sisi dinding tersebut memenuhi persamaan teorema Pythagoras.
5. Pemetaan dan Navigasi
Dalam pemetaan dan navigasi, teorema Pythagoras digunakan untuk menghitung jarak antara dua titik dalam sistem koordinat.
Misalnya, dengan mengetahui koordinat dua titik, kita dapat menggunakan teorema Pythagoras untuk menghitung jarak lurus antara kedua titik tersebut.
6. Fisika
Dalam fisika, teorema Pythagoras digunakan dalam berbagai konteks, seperti menghitung gaya atau vektor secara komponen atau menghitung jalur atau lintasan objek yang bergerak dalam ruang tiga dimensi.
7. Astronomi
Teorema Pythagoras digunakan dalam pengukuran jarak antara benda-benda langit, seperti menghitung jarak antara planet atau bintang berdasarkan sudut pengamatan.
Penggunaan teorema Pythagoras tidak terbatas pada bidang-bidang di atas. Teorema ini memiliki aplikasi yang luas dalam matematika, ilmu pengetahuan, dan kehidupan sehari-hari.
Pemahaman yang baik tentang teorema Pythagoras sangat penting dalam banyak bidang ilmu untuk mengatasi berbagai masalah yang melibatkan segitiga siku-siku dan pengukuran jarak serta sudut.
Bunyi Teorema Pythagoras
Teorema Pythagoras dapat dirumuskan dalam kata-kata sebagai berikut:
“Di dalam segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi yang membentuk sudut siku.”
Dengan kata lain, jika �a dan �b adalah panjang dua sisi yang membentuk sudut siku dalam segitiga, dan �c adalah panjang sisi miring (hipotenusa), maka teorema Pythagoras menyatakan:
“Panjang hipotenusa �c dalam segitiga siku-siku adalah hasil akar kuadrat dari jumlah kuadrat panjang sisi-sisi yang membentuk sudut siku, yaitu �2+�2a2+b2.”
Secara matematis, teorema Pythagoras dapat dirumuskan sebagai:
�2=�2+�2c2=a2+b2
Dalam rumus ini:
- �c adalah panjang sisi miring (hipotenusa).
- �a adalah panjang salah satu sisi yang membentuk sudut siku.
- �b adalah panjang sisi lainnya yang juga membentuk sudut siku.
Teorema Pythagoras adalah dasar dalam geometri yang digunakan untuk menghitung panjang sisi dalam segitiga siku-siku dan memiliki banyak aplikasi dalam berbagai bidang matematika dan ilmu pengetahuan lainnya.
Rumus Teorema Pythagoras
Rumus Teorema Pythagoras adalah sebagai berikut:
Dalam sebuah segitiga siku-siku, jika panjang sisi-sisi yang membentuk sudut siku-siku adalah a dan b, dan panjang hipotenusa adalah c, maka berlaku persamaan:
a^2 + b^2 = c^2
Dalam rumus di atas, a^2 dan b^2 adalah kuadrat dari panjang sisi-sisi yang membentuk sudut siku-siku, sedangkan c^2 adalah kuadrat dari panjang hipotenusa.
Untuk menggunakan rumus ini, kita harus mengkuadratkan panjang sisi-sisi dan kemudian menjumlahkan hasilnya. Hasil penjumlahan tersebut akan sama dengan kuadrat panjang hipotenusa.
Rumus ini dapat digunakan untuk mencari panjang sisi yang tidak diketahui dalam segitiga siku-siku, jika panjang sisi-sisi lainnya diketahui.
Misalnya, jika panjang sisi a dan b diketahui, kita dapat menggunakan rumus ini untuk mencari panjang hipotenusa c. Atau jika panjang sisi a dan c diketahui, kita dapat menggunakan rumus ini untuk mencari panjang sisi b.
Rumus Teorema Pythagoras adalah dasar dari segitiga siku-siku dan digunakan secara luas dalam matematika, fisika, arsitektur, dan berbagai bidang lainnya.
Tabel Tripel Pythagoras
Tabel Tripel Pythagoras, juga dikenal sebagai “tripel Pythagorean” atau “tripel siku-siku”, adalah kumpulan angka bulat positif (a, b, c) yang memenuhi Teorema Pythagoras (a^2 + b^2 = c^2). Tabel ini berisi kombinasi angka-angka tersebut yang membentuk segitiga siku-siku.
Berikut adalah beberapa contoh tripel Pythagoras yang umum:
1. (3, 4, 5)
Tripel ini merupakan tripel Pythagoras paling sederhana dan terkenal. Jika kita menggantikan a = 3, b = 4, dan c = 5 ke dalam rumus Teorema Pythagoras, maka akan memenuhi persamaan 3^2 + 4^2 = 5^2.
2. (5, 12, 13)
Tripel ini juga sangat umum dan memiliki perbandingan sisi 3:4:5. Menggantikan a = 5, b = 12, dan c = 13 ke dalam rumus Teorema Pythagoras, akan memenuhi persamaan 5^2 + 12^2 = 13^2.
3. (8, 15, 17)
Tripel ini memiliki perbandingan sisi 8:15:17. Jika kita menggantikan a = 8, b = 15, dan c = 17 ke dalam rumus Teorema Pythagoras, akan memenuhi persamaan 8^2 + 15^2 = 17^2.
4. (7, 24, 25)
Tripel ini juga memiliki perbandingan sisi 7:24:25. Jika kita menggantikan a = 7, b = 24, dan c = 25 ke dalam rumus Teorema Pythagoras, akan memenuhi persamaan 7^2 + 24^2 = 25^2.
5. (9, 40, 41)
Tripel ini memiliki perbandingan sisi 9:40:41. Menggantikan a = 9, b = 40, dan c = 41 ke dalam rumus Teorema Pythagoras, akan memenuhi persamaan 9^2 + 40^2 = 41^2.
Tabel Tripel Pythagoras dapat diperluas hingga angka yang lebih besar dengan tetap memenuhi Teorema Pythagoras.
Tripel-tripel tersebut digunakan dalam berbagai konteks matematika, fisika, dan bidang lainnya untuk memecahkan masalah dan perhitungan yang melibatkan segitiga siku-siku.
Penerapan Rumus Pythagoras
Rumus Pythagoras memiliki banyak penerapan praktis dalam berbagai bidang. Berikut adalah beberapa contoh penerapannya:
1. Mencari panjang sisi segitiga siku-siku
Rumus Pythagoras dapat digunakan untuk mencari panjang sisi yang tidak diketahui dalam segitiga siku-siku.
Jika panjang dua sisi diketahui, kita dapat menghitung panjang sisi ketiga dengan menggunakan rumus Pythagoras.
2. Membuktikan bahwa suatu segitiga adalah segitiga siku-siku
Rumus Pythagoras juga digunakan untuk membuktikan apakah suatu segitiga merupakan segitiga siku-siku.
Jika panjang sisi-sisi segitiga memenuhi persamaan Pythagoras (a^2 + b^2 = c^2), maka segitiga tersebut dapat diklasifikasikan sebagai segitiga siku-siku.
3. Menghitung jarak
Rumus Pythagoras digunakan dalam pemetaan dan navigasi untuk menghitung jarak antara dua titik dalam sistem koordinat.
Dengan mengetahui koordinat dua titik, kita dapat menggunakan rumus Pythagoras untuk menghitung jarak lurus antara kedua titik tersebut.
4. Menghitung kedalaman
Rumus Pythagoras dapat digunakan dalam pengukuran kedalaman dan kemiringan. Misalnya, dalam surveying, jika kita memiliki sudut kemiringan dan jarak horizontal, kita dapat menggunakan rumus Pythagoras untuk menghitung kedalaman atau jarak vertikal.
5. Membuat desain bangunan
Rumus Pythagoras digunakan dalam arsitektur dan konstruksi untuk memastikan sudut-sudut yang tepat dan proporsi yang seimbang dalam desain bangunan.
Misalnya, untuk membangun dinding dengan sudut 90 derajat, rumus Pythagoras digunakan untuk memastikan panjang sisi-sisi dinding memenuhi persamaan Pythagoras.
6. Menghitung vektor
Dalam fisika dan matematika, rumus Pythagoras digunakan untuk menghitung vektor. Vektor merupakan besaran yang memiliki arah dan magnitudo.
Untuk menghitung panjang atau magnitudo vektor, kita dapat menggunakan rumus Pythagoras pada komponen-komponen vektor dalam sistem koordinat.
7. Aplikasi dalam teknologi
Rumus Pythagoras digunakan dalam berbagai aplikasi teknologi, seperti pemrosesan citra, grafika komputer, dan pemodelan 3D.
Misalnya, dalam rendering grafis, rumus Pythagoras digunakan untuk menghitung jarak antara kamera dan objek untuk menentukan tampilan perspektif yang realistis.
Rumus Pythagoras memiliki penerapan yang luas dalam berbagai bidang ilmu dan digunakan dalam berbagai konteks untuk memecahkan masalah, menghitung jarak, dan mendapatkan informasi yang penting dalam berbagai situasi.
Contoh Soal Pythagoras dan Penyelesaiannya
Tentu! Berikut ini adalah beberapa contoh soal Pythagoras beserta penyelesaiannya:
Contoh Soal 1
Sebuah segitiga siku-siku memiliki panjang sisi-sisi a = 5 cm dan b = 12 cm. Hitunglah panjang sisi hipotenusa (c).
Penyelesaian:
Kita dapat menggunakan rumus Pythagoras (a^2 + b^2 = c^2) untuk mencari panjang sisi hipotenusa.
a = 5 cm b = 12 cm
a^2 + b^2 = c^2 5^2 + 12^2 = c^2 25 + 144 = c^2 169 = c^2
Kuadratkan kedua sisi persamaan untuk mendapatkan:
c = √169 c = 13 cm
Jadi, panjang sisi hipotenusa (c) adalah 13 cm.
Contoh Soal 2
Sebuah tangga memiliki tinggi 9 meter dan jarak dari pangkal tangga ke dinding adalah 12 meter. Berapa panjang tangga tersebut?
Penyelesaian:
Dalam hal ini, tinggi tangga dan jarak dari pangkal tangga ke dinding adalah panjang sisi-sisi a dan b dalam rumus Pythagoras. Panjang tangga (c) adalah hipotenusa.
a = 9 meter b = 12 meter
a^2 + b^2 = c^2 9^2 + 12^2 = c^2 81 + 144 = c^2 225 = c^2
Kuadratkan kedua sisi persamaan untuk mendapatkan:
c = √225 c = 15 meter
Jadi, panjang tangga tersebut adalah 15 meter.
Contoh Soal 3
Sebuah segitiga siku-siku memiliki panjang sisi-sisi a = 3 cm dan c = 5 cm. Hitunglah panjang sisi b.
Penyelesaian:
Kita dapat menggunakan rumus Pythagoras (a^2 + b^2 = c^2) untuk mencari panjang sisi yang tidak diketahui.
a = 3 cm c = 5 cm
a^2 + b^2 = c^2 3^2 + b^2 = 5^2 9 + b^2 = 25 b^2 = 25 – 9 b^2 = 16
Kuadratkan kedua sisi persamaan untuk mendapatkan:
b = √16 b = 4 cm
Jadi, panjang sisi b adalah 4 cm.
Contoh Soal 4
Sebuah taman berbentuk segitiga siku-siku dengan panjang sisi-sisi a = 8 m dan b = 15 m. Hitunglah panjang sisi hipotenusa dan tinggi taman.
Penyelesaian:
Kita dapat menggunakan rumus Pythagoras untuk mencari panjang sisi hipotenusa dan tinggi taman.
a = 8 m b = 15 m
a^2 + b^2 = c^2 8^2 + 15^2 = c^2 64 + 225 = c^2 289 = c^2
Kuadratkan kedua sisi persamaan untuk mendapatkan:
c = √289 c = 17 m
Jadi, panjang sisi hipotenusa (c) adalah 17 m.
Untuk mencari tinggi taman, kita dapat menggunakan salah satu panjang sisi (a atau b) dan rumus Pythagoras.
Misalnya, kita gunakan panjang sisi a = 8 m.
a^2 + tinggi^2 = c^2 8^2 + tinggi^2 = 17^2 64 + tinggi^2 = 289 tinggi^2 = 289 – 64 tinggi^2 = 225
Kuadratkan kedua sisi persamaan untuk mendapatkan:
tinggi = √225 tinggi = 15 m
Jadi, tinggi taman adalah 15 m.
Semoga contoh soal dan penyelesaiannya di atas membantu Anda memahami cara mengaplikasikan rumus Pythagoras dalam pemecahan masalah segitiga siku-siku.
Demikian artikel kali ini. Semoga artikel ini dapat membantu kamu untuk mempelajari Teorema Pythagoras lebih baik lagi. Sampai jumpa di artikel selanjutnya.
Baca juga artikel lainnya :
- Pengertian Ragam Hias : Pola, Skema, Alat dan Tekniknya
- Pengertian PPOB : Manfaat dan Cara Membangun PPOBnya
- Pengertian Konsolidasi : Arah, Ciri, Dampak dan Contohnya
- Pengertian Kesehatan : Aspek, Tujuan dan Ruang Lingkupnya
- Pengertian Restitusi: Aturan, Tujuan, Syarat dan Tata Caranya
- Pengertian Persamaan Diferensial: Jenis dan Penyelesaiannya