Pengertian Integral : Notasi, Konsep, Rumus dan Jenisnya

Pengertian Integral – Integral adalah salah satu konsep matematika yang sangat penting dan luas dalam berbagai disiplin ilmu.

Konsep ini memungkinkan kita untuk menghitung luas daerah di bawah kurva, menentukan total akumulasi perubahan, serta memecahkan berbagai masalah matematika dan ilmu pengetahuan lainnya.

Artikel ini akan menguraikan konsep dasar integral, jenis-jenisnya, dan peran integral dalam matematika serta ilmu pengetahuan lainnya.

Apa Itu Integral?

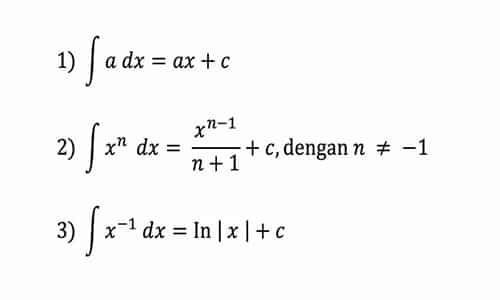
Integral adalah konsep matematika yang digunakan untuk mengukur dan menghitung area di bawah sebuah kurva atau melacak perubahan suatu besaran dalam konteks kalkulus.

Integral dapat digunakan untuk menemukan luas daerah di bawah kurva fungsi, menentukan total akumulasi perubahan dalam suatu proses, dan melakukan berbagai perhitungan matematis yang melibatkan konsep perubahan berkelanjutan.

Terdapat dua jenis integral utama dalam matematika:

1. Integral Tak Tentu (Indefinite Integral)

Juga dikenal sebagai antiderivatif, integral tak tentu adalah operasi yang memberikan fungsi sebagai hasilnya. Ini adalah kebalikan dari diferensiasi.

Integral tak tentu digunakan untuk mencari fungsi yang memiliki turunan yang sama dengan fungsi asal. Notasi umumnya adalah:∫ f(x) dxDi sini, ∫ adalah simbol integral, f(x) adalah fungsi yang akan diintegrasikan, dx menunjukkan variabel terhadap mana fungsi diintegrasikan, dan hasilnya adalah fungsi antiderivatif dari f(x).

2. Integral Tentu (Definite Integral)

Integral tentu digunakan untuk menghitung jumlah total perubahan dalam suatu interval tertentu atau untuk mengukur luas daerah di bawah kurva fungsi dalam interval tersebut.

Notasi integral tentu adalah:∫[a, b] f(x) dxDi sini, [a, b] adalah batas interval, f(x) adalah fungsi yang akan diintegrasikan, dx menunjukkan variabel terhadap mana fungsi diintegrasikan, dan hasilnya adalah angka yang mewakili total akumulasi perubahan dalam interval [a, b].

Integral adalah konsep yang sangat penting dalam matematika dan memiliki berbagai aplikasi dalam ilmu pengetahuan, teknik, ekonomi, fisika, dan berbagai bidang lainnya.

Dalam kalkulus, integral dan diferensiasi adalah dua operasi dasar yang saling berhubungan dan digunakan untuk memahami perubahan, perhitungan area, dan berbagai masalah matematis lainnya.

Notasi Integral

Notasi integral adalah representasi simbolik dari operasi integral dalam matematika. Notasi ini memungkinkan kita untuk menyajikan fungsi yang akan diintegralkan, variabel integrasi, dan batas-batas integrasi dengan cara yang jelas dan konsisten.

Simbol utama dalam notasi integral adalah simbol integral (∫), yang menandakan bahwa operasi integral sedang dilakukan.

Berikut adalah komponen-komponen utama dalam notasi integral:

1. Simbol Integral

Simbol integral ditandai oleh simbol ∫ yang terdiri dari garis horizontal dan lingkaran pada salah satu ujungnya. Simbol ini menunjukkan bahwa operasi integral sedang dilakukan.

2. Fungsi yang Akan Diintegralkan

Fungsi yang akan diintegralkan ditulis di sebelah kanan simbol integral. Fungsi ini dapat dinyatakan dalam bentuk f(x), y = f(x), atau notasi lain yang sesuai dengan konteks masalah.

Misalnya, jika kita ingin mengintegralkan fungsi f(x) = x^2, maka fungsi tersebut akan ditulis di sebelah kanan simbol integral.

3. Variabel Integrasi

Variabel integrasi ditulis di sebelah kanan simbol integral dan biasanya berada di bawahnya. Variabel ini digunakan untuk mengindikasikan variabel yang dianggap sebagai variabel independen dalam operasi integral.

Variabel ini biasanya ditulis sebagai x, tetapi juga dapat menggunakan variabel lain seperti t atau θ tergantung pada konteks masalah.

Misalnya, jika kita ingin mengintegralkan fungsi f(x) = x^2 dengan variabel integrasi x, maka variabel x akan ditulis di bawah simbol integral.

4. Batas-batas Integrasi

Batas-batas integrasi menentukan interval di mana operasi integral dilakukan. Batas-batas ini ditulis sebagai a dan b di sebelah simbol integral.

Batas bawah a menunjukkan titik awal interval, sedangkan batas atas b menunjukkan titik akhir interval. Misalnya, jika kita ingin mengintegralkan fungsi f(x) = x^2 dari x = 0 hingga x = 2, maka batas-batas integrasi akan ditulis sebagai ∫[0, 2].

Secara keseluruhan, notasi integral dapat ditulis dalam bentuk berikut:

∫ f(x) dx

di mana f(x) adalah fungsi yang akan diintegralkan, dx adalah variabel integrasi, dan batas-batas integrasi dapat ditambahkan jika diperlukan.

Notasi integral ini membantu dalam menyajikan operasi integral dengan jelas dan mempermudah dalam melakukan perhitungan matematika yang melibatkan integral.

Konsep Integral

Konsep integral adalah salah satu konsep utama dalam kalkulus yang memungkinkan kita untuk menghitung luas daerah di bawah kurva, menemukan nilai rata-rata suatu fungsi, menghitung total akumulasi suatu fungsi, dan melakukan banyak perhitungan matematika yang berhubungan dengan jumlah berkelanjutan atau kontinu.

Ada dua jenis integral yang umum dalam kalkulus: integral tak tentu (indefinite integral) dan integral tentu (definite integral).

Integral tak tentu, atau sering disebut antiturunan, adalah kebalikan dari operasi diferensiasi. Jika kita memiliki fungsi f(x), integral tak tentu dari f(x) dengan variabel x adalah suatu fungsi F(x) yang memenuhi aturan F'(x) = f(x).

Integral tak tentu biasanya dinyatakan dengan simbol ∫ f(x) dx, di mana f(x) adalah fungsi yang diintegralkan dan dx menunjukkan diferensial dari variabel x.

Integral tentu, di sisi lain, menghitung luas daerah di bawah kurva fungsi dalam interval yang ditentukan. Integral tentu dari suatu fungsi f(x) di antara dua titik a dan b, dinyatakan sebagai ∫[a, b] f(x) dx. Hasil integral tentu adalah suatu bilangan yang menunjukkan luas daerah di bawah kurva f(x) dari titik a ke titik b.

Integral juga melibatkan konsep partisi atau membagi interval menjadi bagian-bagian yang lebih kecil. Dalam kalkulus, kita menggunakan batas untuk mendekati jumlah kecil ini, dan dengan mengambil batas partisi yang semakin halus, kita dapat mendekati nilai integral secara akurat.

Konsep integral juga terkait erat dengan konsep limit dan turunan. Misalnya, teorema dasar kalkulus menghubungkan antara operasi diferensiasi dan integral.

Teorema ini menyatakan bahwa integral tak tentu dari suatu fungsi f(x) dapat dihitung dengan mencari fungsi F(x) yang merupakan antiturunan dari f(x) dan kemudian mengambil selisih F(b) – F(a), di mana a dan b adalah batas integrasi.

Integral memiliki banyak aplikasi dalam matematika, fisika, ekonomi, statistik, dan berbagai bidang ilmu lainnya.

Dengan menggunakan konsep integral, kita dapat menganalisis perubahan dalam bentuk kontinu, menghitung luas dan volume, menemukan solusi persamaan diferensial, dan banyak lagi.

Integral merupakan salah satu alat penting dalam kalkulus yang memungkinkan kita untuk memahami dan memodelkan fenomena yang melibatkan perubahan kontinu.

Integral Tak Tentu dan Integral Tentu

Integral tak tentu (indefinite integral) dan integral tentu (definite integral) adalah dua konsep dasar dalam matematika yang terkait dengan operasi integral. Meskipun keduanya berhubungan dengan menghitung integral suatu fungsi, ada perbedaan penting dalam hasil yang diberikan.

1. Integral Tak Tentu (Indefinite Integral)

Integral tak tentu adalah operasi integral yang menghasilkan fungsi primitif atau antiderivatif dari fungsi yang diintegralkan. Ini dapat dianggap sebagai kebalikan dari operasi diferensiasi.

Jika F(x) adalah fungsi primitif dari f(x), maka kita menulis:∫ f(x) dx = F(x) + Cdi mana f(x) adalah fungsi yang diintegralkan, F(x) adalah fungsi primitif dari f(x), dx adalah variabel integrasi, ∫ adalah simbol integral, dan C adalah konstanta integrasi.

Penting untuk dicatat bahwa integral tak tentu menghasilkan fungsi umum, dan konstanta integrasi C diperlukan karena fungsi primitif yang dihasilkan dapat memiliki sejumlah tak terhingga fungsi yang berbeda yang merupakan solusi.

2. Integral Tentu (Definite Integral)

Integral tentu adalah operasi integral yang menghasilkan nilai numerik yang menunjukkan total akumulasi fungsi dalam suatu interval tertentu. Dalam integral tentu, batas-batas integrasi ditentukan dan menghasilkan nilai tunggal.

Jika f(x) adalah fungsi yang diintegralkan dan [a, b] adalah interval batas integrasi, maka integral tentu ditulis sebagai:∫[a, b] f(x) dxHasilnya adalah suatu angka tunggal yang menunjukkan total akumulasi atau luas di bawah kurva fungsi f(x) dari titik a ke titik b.

Nilai integral tentu dapat dihitung menggunakan berbagai metode, seperti metode Riemann, aturan dasar integral, atau teknik-teknik khusus seperti substitusi atau integrasi parsial.

Penting untuk dicatat bahwa dalam integral tentu, tidak ada konstanta integrasi karena hasilnya adalah nilai numerik yang diperoleh dengan menghitung luas atau total akumulasi fungsi dalam interval yang ditentukan.

Perbedaan utama antara integral tak tentu dan integral tentu adalah hasil yang diberikan. Integral tak tentu menghasilkan fungsi primitif dari fungsi yang diintegralkan, sementara integral tentu menghasilkan nilai numerik yang menunjukkan total akumulasi fungsi dalam interval tertentu.

Metode Perhitungan Integral

Ada beberapa metode yang digunakan dalam perhitungan integral, tergantung pada jenis fungsi yang diintegralkan dan kompleksitasnya. Berikut ini beberapa metode umum yang digunakan:

1. Metode Aturan Dasar Integral

Metode ini merupakan metode dasar yang digunakan untuk menghitung integral fungsi-fungsi dasar. Aturan dasar integral meliputi:

Integral konstanta: ∫ k dx = kx + C, di mana k adalah konstanta.
Integral fungsi pangkat: ∫ x^n dx = (x^(n+1))/(n+1) + C, di mana n bukan -1.
Integral fungsi eksponensial: ∫ e^x dx = e^x + C.
Integral fungsi trigonometri: ∫ sin(x) dx = -cos(x) + C, ∫ cos(x) dx = sin(x) + C, dan sebagainya.

2. Metode Substitusi

Metode substitusi (substitution method) digunakan ketika integral memiliki bentuk yang lebih kompleks.

Dalam metode ini, dilakukan substitusi variabel baru untuk menyederhanakan integral. Beberapa langkah yang umum dilakukan dalam metode substitusi adalah:

Mengganti variabel dengan variabel baru.
Menghitung diferensial variabel baru.
Mengganti fungsi dan diferensial variabel lama dengan fungsi dan diferensial variabel baru.
Menyelesaikan integral baru.
Mengganti kembali variabel baru dengan variabel lama.

3. Metode Integrasi Parsial

Metode integrasi parsial (integration by parts) digunakan untuk mengintegralkan produk dari dua fungsi. Metode ini melibatkan aplikasi aturan dasar diferensiasi dan aturan dasar integral secara bergantian.

Dalam metode integrasi parsial, kita memilih dua fungsi yang akan diintegralkan dan mengggunakan rumus berikut: ∫ u dv = uv – ∫ v du di mana u dan v adalah fungsi-fungsi yang dipilih.

4. Metode Pecahan Parsial

Metode pecahan parsial (partial fractions) digunakan untuk mengintegralkan pecahan rasional yang kompleks.

Dalam metode ini, pecahan rasional didekomposisi menjadi pecahan-pecahan yang lebih sederhana menggunakan aljabar. Setelah pecahan dipecah, integral masing-masing pecahan dapat dihitung secara terpisah.

5. Metode Numerik

Metode numerik digunakan ketika integral tidak dapat dihitung secara analitik. Metode numerik melibatkan pendekatan numerik untuk mengestimasi nilai integral dengan menggunakan teknik seperti metode trapesium, metode Simpson, atau metode Monte Carlo.

Selain metode-metode di atas, ada pula teknik lain seperti integral tak tentu melalui tabel integral, integral trigonometri khusus, integral lipat, dan metode-metode khusus lainnya yang dikembangkan untuk mengatasi situasi-situasi yang lebih kompleks.

Pilihan metode yang tepat tergantung pada sifat fungsi yang akan diintegralkan dan tujuan perhitungan yang diinginkan.

Aplikasi Integral

Integral memiliki banyak aplikasi penting dalam berbagai bidang. Berikut adalah beberapa contoh aplikasi integral:

1. Perhitungan Luas dan Volume

Salah satu aplikasi paling umum dari integral adalah menghitung luas daerah di bawah kurva. Dengan menggunakan integral, kita dapat menemukan luas wilayah yang dibatasi oleh kurva dan sumbu x atau sumbu y.

Selain itu, integral juga digunakan untuk menghitung volume benda tiga dimensi, seperti balok, tabung, kerucut, dan bola, dengan menggunakan metode integral berdasarkan sejajar sumbu.

2. Fisika dan Mekanika

Integral digunakan secara luas dalam fisika dan mekanika untuk menghitung berbagai parameter penting.

Misalnya, dalam kinematika, integral dapat digunakan untuk menghitung jarak tempuh, kecepatan, dan percepatan berdasarkan fungsi waktu.

Dalam dinamika, integral digunakan untuk menghitung gaya, momentum, dan energi. Integral juga diterapkan dalam bidang optik, termodinamika, elektromagnetisme, dan banyak bidang fisika lainnya.

3. Ekonomi dan Keuangan

Integral memiliki aplikasi penting dalam bidang ekonomi dan keuangan. Misalnya, dalam ekonomi mikro, integral digunakan untuk menghitung surplus konsumen atau produsen.

Dalam ekonomi makro, integral digunakan dalam perhitungan agregat ekonomi seperti pendapatan nasional, investasi, atau konsumsi.

Di bidang keuangan, integral digunakan untuk menghitung harga opsi, nilai saat ini arus kas, atau risiko portofolio.

4. Statistik dan Probabilitas

Integral juga diterapkan dalam statistik dan probabilitas. Dalam statistik, integral digunakan dalam perhitungan distribusi probabilitas, estimasi parameter, dan pengujian hipotesis.

Dalam probabilitas, integral digunakan untuk menghitung probabilitas kejadian yang kompleks dengan menggunakan fungsi distribusi probabilitas. Misalnya, integral digunakan dalam perhitungan probabilitas dalam distribusi normal atau distribusi eksponensial.

5. Teori Kontrol dan Rekayasa

Integral digunakan dalam teori kontrol dan rekayasa untuk menghitung respons sistem dinamik. Dalam kontrol sistem, integral digunakan dalam perhitungan fungsi transfer dan perancangan kontroler.

Dalam rekayasa, integral digunakan dalam perhitungan daya, energi, dan karakteristik sistem yang melibatkan variabel yang berubah seiring waktu.

6. Ilmu Komputer dan Grafika Komputer

Integral juga memiliki aplikasi dalam ilmu komputer dan grafika komputer. Misalnya, integral digunakan dalam perhitungan grafika komputer untuk menghasilkan efek pencahayaan dan bayangan yang realistis. Integral juga digunakan dalam pemrosesan sinyal, pengolahan citra, dan kompresi data.

Selain contoh-contoh di atas, integral juga memiliki banyak aplikasi dalam ilmu biologi, kimia, lingkungan, ilmu material, dan banyak bidang lainnya.

Integral memungkinkan kita untuk menggambarkan dan menganalisis berbagai fenomena yang kontinu dan kompleks, serta memberikan alat yang kuat dalam pemodelan matematika.

Sifat Integral

Integral memiliki beberapa sifat penting yang memudahkan dalam penggunaannya dan memungkinkan untuk menyelesaikan berbagai masalah matematis. Berikut adalah beberapa sifat integral yang paling penting:

1. Sifat Linear

Integral adalah operasi linear, yang berarti bahwa integral dari jumlah atau selisih dua fungsi sama dengan jumlah atau selisih integral masing-masing fungsi tersebut.

Dalam notasi, ini dapat ditulis sebagai berikut:∫[a, b] [f(x) + g(x)] dx = ∫[a, b] f(x) dx + ∫[a, b] g(x) dx ∫[a, b] [f(x) – g(x)] dx = ∫[a, b] f(x) dx – ∫[a, b] g(x) dx

2. Konstanta Keluar dari Integral

Ketika kita mengintegrasikan konstanta, kita dapat mengeluarkannya dari integral. Ini berarti bahwa jika “c” adalah konstanta, maka:∫[a, b] c * f(x) dx = c * ∫[a, b] f(x) dx

3. Pemisahan Interval

Jika kita memiliki interval yang terbagi menjadi beberapa bagian, kita dapat mengintegrasikan fungsi dalam interval tersebut secara terpisah, dan kemudian menjumlahkan hasilnya. Ini dikenal sebagai sifat pemisahan integral:∫[a, b] f(x) dx = ∫[a, c] f(x) dx + ∫[c, b] f(x) dx

4. Integral dari Nol

Integral dari fungsi konstan atau nol dalam interval tertentu adalah nol:∫[a, b] 0 dx = 0

5. Perubahan Batas

Jika kita mengubah batas integral dari [a, b] ke [c, d], hasil integralnya tetap sama jika fungsi yang diintegrasikan tetap sama:∫[a, b] f(x) dx = ∫[c, d] f(x) dx

6. Ketentuan Perbandingan

Jika f(x) kurang dari atau sama dengan g(x) dalam interval [a, b], maka integral dari f(x) dalam interval tersebut kurang dari atau sama dengan integral dari g(x):Jika f(x) ≤ g(x) untuk setiap x di [a, b], maka ∫[a, b] f(x) dx ≤ ∫[a, b] g(x) dx

7. Sifat Invers

Integral dari turunan suatu fungsi adalah fungsi itu sendiri (antiderivatif). Dalam notasi ini disebut “Teorema Fundamental Kalkulus.”∫[a, b] f'(x) dx = F(b) – F(a)Di sini, F(x) adalah antiderivatif dari f(x).

8. Simetri Integral

Jika fungsi f(x) adalah fungsi simetris terhadap titik tengah interval [a, b], maka integral dari f(x) dalam interval tersebut adalah nol.Jika f(x) adalah fungsi simetris terhadap titik tengah (a + b) / 2, maka ∫[a, b] f(x) dx = 0

Sifat-sifat ini membantu dalam menghitung integral dan menganalisis fungsi dalam berbagai konteks matematika dan ilmu pengetahuan lainnya.

Dengan memahami sifat-sifat ini, kita dapat melakukan berbagai manipulasi matematis yang berguna dalam menyelesaikan masalah integral.

Subtitusi Integral

Substitusi integral, juga dikenal sebagai metode perubahan variabel, adalah teknik dalam kalkulus yang digunakan untuk menyederhanakan integral dengan mengganti variabel integral dengan variabel baru.

Metode ini berguna ketika integral memiliki bentuk yang kompleks atau sulit diintegralkan secara langsung.

Langkah-langkah umum dalam substitusi integral adalah sebagai berikut:

1. Pilih Substitusi

Pilih variabel baru yang akan menggantikan variabel dalam integral. Variabel baru ini biasanya dipilih berdasarkan bagian dari integral yang kompleks atau memiliki turunan yang dapat disederhanakan.

2. Hitung Diferensial Variabel Baru

Diferensiasikan variabel baru untuk mendapatkan diferensial variabel baru. Dalam banyak kasus, diferensial variabel baru dapat ditemukan dengan menggunakan aturan dasar diferensiasi.

3. Terapkan Substitusi

Ganti variabel dalam integral dengan variabel baru yang telah ditentukan, termasuk diferensial variabel. Sesuaikan batas integral jika perlu.

4. Simplifikasikan Integral

Simplifikasikan integral dengan menggunakan substitusi yang telah diterapkan. Dalam banyak kasus, substitusi akan mengubah integral yang awalnya kompleks menjadi integral yang lebih sederhana.

5. Hitung Integral Baru

Hitung integral baru dengan menggunakan metode integral yang sesuai. Jika berhasil melakukan substitusi yang tepat, integral baru akan menjadi lebih mudah diintegralkan atau dapat diidentifikasi sebagai integral standar yang telah diketahui solusinya.

6. Kembalikan Variabel Awal

Jika telah selesai menghitung integral baru, kembalikan variabel awal dengan mengganti variabel baru dengan variabel asli dalam solusi integral. Jangan lupa untuk mengganti diferensial variabel baru dengan diferensial variabel asli juga.

Substitusi integral memungkinkan kita untuk mengubah bentuk integral yang kompleks menjadi bentuk yang lebih mudah diintegralkan atau dikenal solusinya.

Dengan memilih substitusi yang tepat, kita dapat menyederhanakan proses perhitungan dan meningkatkan efisiensi dalam menyelesaikan integral.

Penting untuk berlatih dalam pemilihan substitusi yang tepat dan melihat pola-pola umum dalam integral untuk mengenali kesempatan penggunaan metode ini.

Jenis-jenis Integral

Dalam kalkulus, terdapat beberapa jenis integral yang umum digunakan. Berikut adalah beberapa jenis integral yang penting:

1. Integral Tak Tentu (Indefinite Integral)

Integral tak tentu, juga dikenal sebagai antiturunan, adalah kebalikan dari operasi diferensiasi. Integral tak tentu dari suatu fungsi f(x) dengan variabel x dinyatakan sebagai ∫ f(x) dx, di mana f(x) adalah fungsi yang diintegralkan dan dx menunjukkan diferensial dari variabel x.

Integral tak tentu menghasilkan fungsi baru, dan konstanta integrasi (C) ditambahkan untuk memperhitungkan semua konstanta yang hilang dalam proses integrasi.

2. Integral Tentu (Definite Integral)

Integral tentu menghitung luas daerah di bawah kurva fungsi dalam interval yang ditentukan. Integral tentu dari suatu fungsi f(x) di antara dua titik a dan b dinyatakan sebagai ∫[a, b] f(x) dx.

Integral tentu menghasilkan suatu bilangan yang menunjukkan luas daerah di bawah kurva f(x) dari titik a ke titik b. Hasil integral tentu tidak lagi mengandung konstanta integrasi.

3. Integral Improper (Integral Tak Wajar)

Integral tak wajar adalah jenis integral tentu di mana batas integrasi adalah tak terhingga atau fungsi yang tidak terbatas pada interval tertentu.

Integral tak wajar muncul ketika fungsi yang diintegralkan memiliki singularitas atau divergensi. Untuk menghitung integral tak wajar, kita harus menggunakan limit saat batas integrasi mendekati tak terhingga atau titik singuler.

4. Integral Ganda

Integral ganda adalah integral dari suatu fungsi dua variabel terhadap dua variabel tersebut. Integral ganda biasanya digunakan untuk menghitung volume di dalam ruang tiga dimensi atau luas daerah di dalam bidang dua dimensi.

Integral ganda dituliskan sebagai ∬ f(x, y) dA, di mana f(x, y) adalah fungsi yang diintegralkan dan dA menunjukkan elemen luas atau volume.

5. Integral Permukaan

Integral permukaan adalah integral dari suatu fungsi terhadap permukaan dalam ruang tiga dimensi. Integral permukaan digunakan untuk menghitung luas permukaan benda tiga dimensi atau menghitung aliran medan vektor melalui permukaan tertentu.

Integral permukaan dituliskan sebagai ∬ f(x, y, z) dS, di mana f(x, y, z) adalah fungsi yang diintegralkan dan dS menunjukkan elemen luas permukaan.

6. Integral Lintasan

Integral lintasan, juga dikenal sebagai integral garis, adalah integral dari suatu fungsi terhadap kurva atau lintasan dalam ruang tiga dimensi.

Integral lintasan digunakan untuk menghitung panjang lengkungan kurva atau menghitung pekerjaan yang dilakukan oleh medan vektor di sepanjang lintasan tertentu.

Integral lintasan dituliskan sebagai ∫ f(x, y, z) ds, di mana f(x, y, z) adalah fungsi yang diintegralkan dan ds menunjukkan elemen panjang lintasan.

Jenis-jenis integral tersebut memungkinkan kita untuk mengatasi berbagai perhitungan matematika yang melibatkan luas, volume, panjang lintasan, dan banyak lagi. Setiap jenis integral memiliki aplikasi dan teknik khusus dalam perhitungannya.

Rumus Integral

Rumus integral merupakan rumus matematika yang digunakan untuk menghitung integral dari suatu fungsi. Berikut adalah beberapa rumus integral yang umum digunakan:

1. Integral dari Konstanta

∫ k dx = kx + CRumus ini digunakan ketika mengintegrasikan konstanta, di mana k adalah konstanta dan C adalah konstanta integrasi.

2. Integral dari Fungsi Pangkat

∫ x^n dx = (x^(n+1))/(n+1) + C, untuk n ≠ -1Rumus ini digunakan untuk mengintegrasikan fungsi pangkat, di mana n adalah bilangan riil, kecuali -1.

3. Integral dari Fungsi Eksponensial

∫ e^x dx = e^x + CRumus ini digunakan ketika mengintegrasikan fungsi eksponensial dengan dasar e.

4. Integral dari Fungsi Trigonometri

∫ sin(x) dx = -cos(x) + C ∫ cos(x) dx = sin(x) + C ∫ tan(x) dx = -ln|cos(x)| + CRumus ini digunakan untuk mengintegrasikan fungsi trigonometri seperti sinus, kosinus, dan tangen.

5. Integral dari Fungsi Logaritma

∫ (1/x) dx = ln|x| + CRumus ini digunakan ketika mengintegrasikan fungsi logaritma natural.

6. Integral dengan Substitusi

Jika terdapat substitusi variabel u = g(x), maka integralnya dapat ditulis sebagai ∫ f(g(x)) g'(x) dx = ∫ f(u) du.Rumus ini digunakan ketika melakukan substitusi variabel untuk menyederhanakan integral.

7. Integral dari Fungsi Trigonometri Invers

∫ sec^2(x) dx = tan(x) + C ∫ csc^2(x) dx = -cot(x) + CRumus ini digunakan ketika mengintegrasikan fungsi trigonometri invers seperti sekans kuadrat dan kosekans kuadrat.

8. Integral Parsial

∫ u dv = uv – ∫ v duRumus ini digunakan dalam metode integral parsial untuk mengintegrasikan produk dua fungsi.

Rumus integral di atas hanya beberapa contoh umum. Terdapat pula rumus-rumus integral lainnya yang lebih kompleks tergantung pada jenis fungsi yang diintegralkan.

Penting untuk memahami prinsip-prinsip kalkulus dan teknik-teknik integral yang lebih lanjut untuk menghadapi kasus integral yang lebih kompleks.

Contoh Soal Integral dan Penyelesaiannya

Tentu! Berikut adalah beberapa contoh soal integral beserta penyelesaiannya:

Contoh Soal 1

Hitunglah integral tak tentu dari fungsi f(x) = 3x^2 + 2x – 5.

Penyelesaian:

Untuk menghitung integral tak tentu, kita gunakan rumus integral dari fungsi pangkat: ∫ x^n dx = (x^(n+1))/(n+1) + C.

Dalam kasus ini, fungsi f(x) memiliki pangkat 2, sehingga kita dapat menggunakan rumus tersebut. ∫ (3x^2 + 2x – 5) dx = ∫ 3x^2 dx + ∫ 2x dx – ∫ 5 dx = (3/3)x^3 + (2/2)x^2 – (5x) + C = x^3 + x^2 – 5x + C.

Jadi, integral tak tentu dari fungsi f(x) = 3x^2 + 2x – 5 adalah x^3 + x^2 – 5x + C.

Contoh Soal 2

Hitunglah integral tentu dari fungsi f(x) = 2x^3 – 3x^2 + 4x dalam interval [1, 3].

Penyelesaian:

Untuk menghitung integral tentu, kita gunakan rumus integral tentu: ∫[a, b] f(x) dx = F(b) – F(a), di mana F(x) adalah fungsi antiturunan dari f(x).

Dalam kasus ini, kita perlu mencari antiturunan dari fungsi f(x) terlebih dahulu: F(x) = ∫ (2x^3 – 3x^2 + 4x) dx = (2/4)x^4 – (3/3)x^3 + (4/2)x^2 + C = (1/2)x^4 – x^3 + 2x^2 + C.

Kemudian, kita dapat menghitung integral tentu dengan memasukkan batas integrasi: ∫[1, 3] (2x^3 – 3x^2 + 4x) dx = F(3) – F(1) = [(1/2)(3)^4 – (3)^3 + 2(3)^2 + C] – [(1/2)(1)^4 – (1)^3 + 2(1)^2 + C] = (81/2 – 27 + 18) – (1/2 – 1 + 2) = 81/2 – 27 + 18 – 1/2 + 1 – 2 = 71/2.

Jadi, integral tentu dari fungsi f(x) = 2x^3 – 3x^2 + 4x dalam interval [1, 3] adalah 71/2.

Ini adalah contoh-contoh sederhana dari perhitungan integral tak tentu dan integral tentu. Dalam praktiknya, terdapat berbagai jenis fungsi yang diintegralkan dan teknik yang lebih kompleks yang diperlukan untuk menyelesaikan integral yang lebih rumit.

Demikian artikel kali ini. Semoga artikel ini dapat membantu kamu untuk mempelajari Integral lebih baik lagi. Sampai jumpa di artikel selanjutnya.

Baca juga artikel lainnya :